Author: Julia Jurkowska

Source localization and signal reconstruction - case study for oddball data#

Introduction#

In this tutorial, we will learn how to localize sources from EEG data and reconstruct signals at those sources using MVPURE-py, an extension to MNE-Python. Source localization allows us to move beyond sensor-level analysis to estimate where in the brain the measured activity originates. Once sources are identified, we can reconstruct time series from vertices of interest for further analysis.

We will cover the following steps:

  1. Reading all necessary data for the sample_subject. You can download this dataset here.

  2. Computing data and noise covariance (R and N, respectively).

  3. Analysis of \(RN^{-1}\) eigenvalues to guide the number of sources to localize and select an appropriate optimization parameter.

  4. Localizing the specified number of sources.

  5. Reconstructing source signals for vertices of interest and plotting the results.

All steps will be repeated for two time frames: “sensory” (50-200 ms after stimuli) and “cognitive” (350-600 ms after stimuli).

By the end of this tutorial, you will understand the basic workflow of source localization and signal reconstruction using the MVPURE-py package.

[ ]:

import mne
import os

mne.viz.set_3d_backend('pyvistaqt')

from mvpure_py import localizer, beamformer, viz, utils

We will use data the sample_subject dataset provided on Figshare. If you wish to start from the beginning, please complete tutorial [Preprocessing data from oddball paradigm] first.

[2]:

subject = "sample_subject"
subjects_dir = "subjects"

# Reading mne.Epochs
epoched = mne.read_epochs(os.path.join(subjects_dir, subject, "_eeg", "_pre", f"{subject}_oddball-epo.fif"))
forward_path = os.path.join(subjects_dir, subject, "forward", f"{subject}_ico4-fwd.fif")
trans_path = os.path.join(subjects_dir, subject, "_eeg", "trans", f"{subject}-fit_trans.fif")

# We will be using only data for 'target' stimuli
target = epoched['target']
sel_epoched = target.copy()
sel_epoched = sel_epoched.set_eeg_reference('average', projection=True)
sel_epoched.apply_proj()
sel_evoked = sel_epoched.average()

Reading /Volumes/UMK/oddball/subjects/sample_subject/_eeg/_pre/sample_subject_oddball-epo.fif ...
    Found the data of interest:
        t =    -199.22 ...     800.78 ms
        0 CTF compensation matrices available
Not setting metadata
621 matching events found
No baseline correction applied
0 projection items activated
EEG channel type selected for re-referencing
Adding average EEG reference projection.
1 projection items deactivated
Average reference projection was added, but has not been applied yet. Use the apply_proj method to apply it.
Created an SSP operator (subspace dimension = 1)
1 projection items activated
SSP projectors applied...

To perform source localization, we need a forward model that links activity at source locations to the sensors (in this case EEG channels). Here, we load the forward solution and convert it to a fixed-orientation representation.

[3]:

# Reading mne.Forward
fwd_vector = mne.read_forward_solution(forward_path)

# Using fixed orientation in forward solution
fwd = mne.convert_forward_solution(
    fwd_vector,
    surf_ori=True,
    force_fixed=True,
    use_cps=True
)

# Leadfield matrix
leadfield = fwd["sol"]["data"]

# Source positions extracted from forward model
src = fwd["src"]

Reading forward solution from /Volumes/UMK/oddball/subjects/sample_subject/forward/sample_subject_ico4-fwd.fif...
    Reading a source space...
    [done]
    Reading a source space...
    [done]
    2 source spaces read
    Desired named matrix (kind = 3523 (FIFF_MNE_FORWARD_SOLUTION_GRAD)) not available
    Read EEG forward solution (5124 sources, 128 channels, free orientations)
    Source spaces transformed to the forward solution coordinate frame
    No patch info available. The standard source space normals will be employed in the rotation to the local surface coordinates....
    Changing to fixed-orientation forward solution with surface-based source orientations...
    [done]

“Sensory” processing#

We will start with analysing processes in “sensory” time window.

In an oddball paradigm, participants are presented with a sequence of frequent (standard) and infrequent (target) stimuli. The early neural responses to these target stimuli reflect sensory processing - the brain’s initial registration of the incoming stimulus before higher-level cognitive mechanisms are engaged. We assume that sensory processing for given oddball paradigm occurs within the 50-200 ms window after the stimuli. We will therefore compute the data covariance in this time range. To estimate the noise covariance, we use a baseline period -200ms to 0 ms, i.e., the interval before stimulus onset. This baseline is assumed to be free of stimulus-locked activity and provides reference for separating signal from noise.

[4]:

# Compute noise covariance
noise_cov = mne.compute_covariance(
    sel_epoched,
    tmin=-0.2,
    tmax=0,
    method="empirical"
)

# Compute data covariance for range corresponding to sensory processing
data_cov_sen = mne.compute_covariance(
    sel_epoched,
    tmin=0.05,
    tmax=0.2,
    method="empirical"
)

# Subset signal for given time range
signal_sen = sel_evoked.crop(
    tmin=0.05,
    tmax=0.2
)

    Created an SSP operator (subspace dimension = 1)
    Setting small EEG eigenvalues to zero (without PCA)
Reducing data rank from 128 -> 127
Estimating covariance using EMPIRICAL
Done.
Number of samples used : 4056
[done]
    Created an SSP operator (subspace dimension = 1)
    Setting small EEG eigenvalues to zero (without PCA)
Reducing data rank from 128 -> 127
Estimating covariance using EMPIRICAL
Done.
Number of samples used : 3042
[done]

\(RN^{-1}\) eigenvalues analysis#

Before attempting source localization, we need to decide how many sources to model and with what rank. Our proposition is to analyze the eigenvalues of the product of data covariance matrix \(R\) and the inverse of the noise covariance matrix \(N\). For a detailed theoretical background, see [PAPER].

[5]:

sugg_n_sources, sugg_rank = localizer.suggest_n_sources_and_rank(
    R=data_cov_sen.data,
    N=noise_cov.data,
    show_plot=True,
    subject=subject,
    s=14
)
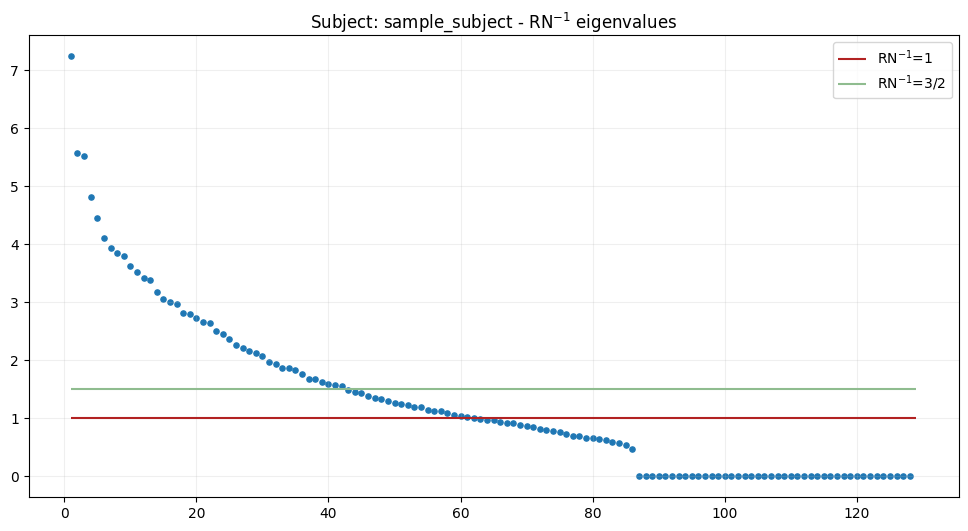
../_images/tutorials_source_localization_and_reconstruction_on_data_from_oddball_paradigm_11_0.png 
Suggested number of sources to localize: 62
Suggested rank is: 42

Localize#

Based on the eigenvalue spectrium above, we will localize 62 sources using rank of 42. We will use function mvpure_py.localizer.localize, which performs the actual source localization. The main parameters are:

  • subject: the subject ID (here: "sample_subject")

  • subjects_dir: directory containing the subject folders.

  • localizer_to_use: the algorithm variant. Here we choose "mpz_mvp" because it provides the highest spacial resolution. Other possible options include: "mai", "mpz", and "mai_mvp". For details, see [PAPER] or the function documentation.

  • n_sources_to_localize: number of sources to localize. We will use the suggested number of sources from \(RN^{-1}\) analysis.

  • R: data covariance matrix

  • N: noise covariance matrix

  • forward: the mne.Forward object for this subject

  • r: optimization rank parameter. We use the suggested value from the eigenvalues analysis, but it can be any integer smaller than number_of_sources_to_localize.

[6]:

locs_sen = localizer.localize(
    subject=subject,
    subjects_dir=subjects_dir,
    localizer_to_use=["mpz_mvp"],
    n_sources_to_localize=sugg_n_sources,
    R=data_cov_sen.data,
    N=noise_cov.data,
    forward=fwd,
    r=sugg_rank
)

Calculating activity index for localizer: mpz_mvp

100%|██████████| 5124/5124 [00:16<00:00, 302.37it/s]
100%|██████████| 5124/5124 [00:16<00:00, 311.68it/s]
100%|██████████| 5124/5124 [00:16<00:00, 311.65it/s]
100%|██████████| 5124/5124 [00:16<00:00, 306.47it/s]
100%|██████████| 5124/5124 [00:16<00:00, 309.97it/s]
100%|██████████| 5124/5124 [00:16<00:00, 307.57it/s]
100%|██████████| 5124/5124 [00:16<00:00, 303.06it/s]
100%|██████████| 5124/5124 [00:16<00:00, 304.61it/s]
100%|██████████| 5124/5124 [00:16<00:00, 303.29it/s]
100%|██████████| 5124/5124 [00:16<00:00, 302.00it/s]
100%|██████████| 5124/5124 [00:17<00:00, 301.35it/s]
100%|██████████| 5124/5124 [00:17<00:00, 295.38it/s]
100%|██████████| 5124/5124 [00:17<00:00, 294.21it/s]
100%|██████████| 5124/5124 [00:17<00:00, 295.95it/s]
100%|██████████| 5124/5124 [00:17<00:00, 293.16it/s]
100%|██████████| 5124/5124 [00:17<00:00, 291.34it/s]
100%|██████████| 5124/5124 [00:18<00:00, 282.57it/s]
100%|██████████| 5124/5124 [00:17<00:00, 287.68it/s]
100%|██████████| 5124/5124 [00:17<00:00, 285.50it/s]
100%|██████████| 5124/5124 [00:19<00:00, 269.37it/s]
100%|██████████| 5124/5124 [00:19<00:00, 268.82it/s]
100%|██████████| 5124/5124 [00:18<00:00, 272.12it/s]
100%|██████████| 5124/5124 [00:18<00:00, 275.31it/s]
100%|██████████| 5124/5124 [00:18<00:00, 278.55it/s]
100%|██████████| 5124/5124 [00:18<00:00, 274.03it/s]
100%|██████████| 5124/5124 [00:18<00:00, 277.67it/s]
100%|██████████| 5124/5124 [00:18<00:00, 272.22it/s]
100%|██████████| 5124/5124 [00:18<00:00, 272.04it/s]
100%|██████████| 5124/5124 [00:18<00:00, 271.20it/s]
100%|██████████| 5124/5124 [00:19<00:00, 266.81it/s]
100%|██████████| 5124/5124 [00:19<00:00, 266.88it/s]
100%|██████████| 5124/5124 [00:19<00:00, 264.43it/s]
100%|██████████| 5124/5124 [00:19<00:00, 264.33it/s]
100%|██████████| 5124/5124 [00:19<00:00, 264.21it/s]
100%|██████████| 5124/5124 [00:19<00:00, 260.33it/s]
100%|██████████| 5124/5124 [00:22<00:00, 231.19it/s]
100%|██████████| 5124/5124 [00:22<00:00, 226.51it/s]
100%|██████████| 5124/5124 [00:22<00:00, 230.34it/s]
100%|██████████| 5124/5124 [00:22<00:00, 231.64it/s]
100%|██████████| 5124/5124 [00:23<00:00, 215.33it/s]
100%|██████████| 5124/5124 [00:30<00:00, 168.64it/s]
100%|██████████| 5124/5124 [00:28<00:00, 181.66it/s]
100%|██████████| 5124/5124 [00:33<00:00, 152.17it/s]
100%|██████████| 5124/5124 [00:34<00:00, 146.65it/s]
100%|██████████| 5124/5124 [00:36<00:00, 141.51it/s]
100%|██████████| 5124/5124 [00:38<00:00, 131.63it/s]
100%|██████████| 5124/5124 [00:39<00:00, 129.57it/s]
100%|██████████| 5124/5124 [00:36<00:00, 139.15it/s]
100%|██████████| 5124/5124 [00:38<00:00, 133.81it/s]
100%|██████████| 5124/5124 [00:38<00:00, 134.63it/s]
100%|██████████| 5124/5124 [00:38<00:00, 133.06it/s]
100%|██████████| 5124/5124 [00:39<00:00, 128.37it/s]
100%|██████████| 5124/5124 [00:37<00:00, 136.43it/s]
100%|██████████| 5124/5124 [00:37<00:00, 137.27it/s]
100%|██████████| 5124/5124 [00:37<00:00, 136.45it/s]
100%|██████████| 5124/5124 [00:38<00:00, 132.86it/s]
100%|██████████| 5124/5124 [00:39<00:00, 129.94it/s]
100%|██████████| 5124/5124 [00:39<00:00, 128.66it/s]
100%|██████████| 5124/5124 [00:40<00:00, 126.19it/s]
100%|██████████| 5124/5124 [00:41<00:00, 123.15it/s]
100%|██████████| 5124/5124 [00:42<00:00, 121.05it/s]
100%|██████████| 5124/5124 [00:45<00:00, 113.27it/s]

Leadfield indices corresponding to localized sources: [31, 3557, 795, 1213, 1690, 2506, 2697, 2602, 1225, 83, 1966, 2085, 994, 2850, 2212, 4404, 4304, 4882, 608, 2522, 2325, 1876, 6, 3255, 1860, 3714, 4804, 2690, 84, 371, 2454, 3624, 5108, 1971, 265, 650, 992, 2727, 42, 4698, 329, 2574, 1258, 4002, 3368, 4920, 3, 33, 1405, 2887, 2333, 2771, 4604, 3333, 302, 306, 4422, 2597, 2580, 16, 4266, 3815]



[7]:

# Transform leadfield indices to vertices
lh_vert_sen, lh_idx_sen, rh_vert_sen, rh_idx_sen = utils.transform_leadfield_indices_to_vertices(
    lf_idx=locs_sen["sources"],
    src=src,
    hemi="both",
    include_mapping=True
)

locs_sen.add_vertices_info(
    lh_vertices=lh_vert_sen,
    lh_indices=lh_idx_sen,
    rh_vertices=rh_vert_sen,
    rh_indices=rh_idx_sen
)

Optionally, we can plot the localized sources on the brain surface:

[8]:

# locs_sen.plot_localized_sources()

Here, the size and color of the markers indicate the order of localization:

  • large, red foci: sources localized earlier

  • small, white foci: sources localized later

Reconstruct#

Now that we have localized sources of interest, the next sgtep is to reconstruct their activity. First, we restrict the original forward model to only include the localized sources. This reduces the forward solution to the relevant subspace:|

[9]:

# Subset mne.Forward
new_fwd_sen = utils.subset_forward(
    old_fwd=fwd,
    localized=locs_sen,
    hemi="both"
)

To compute the filters, we will use beamformer.make_filter.

This function works similarly to mne.beamformer.make_lcmv, but with additional parameters specific to MVPURE.

We provide these in a dictionary called mvpure_params:

  • filter_type: type of the beamformer to use. Options are: MVP_R and MVP_N. In this case, we will use MVP_R as it is generalization of commonly used LCMV filter.

  • filter_rank: optimization rank parameter. For best performance, we use the same rank as in the localization step.

Note: setting filter_rank="full" reduces the method to a standard LCMV filter. For theoretical details see [PAPER].

[10]:

# MVPURE filter parameters
mvpure_params = {
    'filter_type': 'MVP_R',
    'filter_rank': sugg_rank
}

[11]:

# Build beamformer filter (similar to LCMV but with MVPURE options)
filter_sen = beamformer.make_filter(
    signal_sen.info,
    new_fwd_sen,
    data_cov_sen,
    reg=0.05,
    noise_cov=noise_cov,
    pick_ori=None,  # not needed with fixed orientation forward
    weight_norm=None,
    rank=None,
    mvpure_params=mvpure_params
)

Computing rank from covariance with rank=None
    Using tolerance 4.4e-13 (2.2e-16 eps * 128 dim * 15  max singular value)
    Estimated rank (eeg): 86
    EEG: rank 86 computed from 128 data channels with 1 projector
Computing rank from covariance with rank=None
    Using tolerance 3.6e-13 (2.2e-16 eps * 128 dim * 13  max singular value)
    Estimated rank (eeg): 86
    EEG: rank 86 computed from 128 data channels with 1 projector
Making MVP_R beamformer with rank {'eeg': 86} (note: MNE-Python rank)
Computing inverse operator with 128 channels.
    128 out of 128 channels remain after picking
Selected 128 channels
Whitening the forward solution.
    Created an SSP operator (subspace dimension = 1)
Computing rank from covariance with rank={'eeg': 86}
    Setting small EEG eigenvalues to zero (without PCA)
Creating the source covariance matrix
Adjusting source covariance matrix.
Computing beamformer filters for 62 sources
MVP_R computation - in progress...
Filter rank: 42
Filter computation complete

[12]:

# Apply filter to cropped evoked response
stc_sen = beamformer.apply_filter(signal_sen, filter_sen)

We then attach the resulting mne.SourceEstimate to the localized sources object, making it easier to visualize:

[13]:

# Add reconstructed source time course
locs_sen.add_stc(stc_sen)

Finally, let’s plot the localized sources with their reconstructed activity:

[14]:

viz.plot_sources_with_activity(
    subject=subject,
    stc=stc_sen,
    background="white"
)

Using control points [2.91332758e-09 3.43983961e-09 7.89233742e-09]

[14]:

<mne.viz._brain._brain.Brain at 0x1583aa270>

“Cognitive” task#

After examing the early sensory responses, we now turn to the later cognitive stahe of processing in the oddball paradigm. In EEG, target stimuli typically evoke a P300 component — a positive deflection peaking around 300–600 ms after stimulus onset. This response is thought to reflect higher-level cognitive processes, such as attention allocation and stimulus evaluation, in contrast to the earlier sensory responses.

For this dataset, we will therefore define the cognitive time window as 350–600 ms. The pipeline remains the same as before:

  • Compute noise covariance (always from −200 to 0 ms).

  • Compute data covariance in the cognitive window (350–600 ms).

  • Subset the evoked signal to this time range.

[15]:

# Compute data covariance for range corresponding to sensory processing
data_cov_task = mne.compute_covariance(
    sel_epoched,
    tmin=0.35,
    tmax=0.6,
    method="empirical"
)
# There's no need to compute `noise_covariance` again as it is the same time interval

sel_evoked = sel_epoched.average()

# Subset signal for given time range
signal_task = sel_evoked.crop(
    tmin=0.35,
    tmax=0.6
)

    Created an SSP operator (subspace dimension = 1)
    Setting small EEG eigenvalues to zero (without PCA)
Reducing data rank from 128 -> 127
Estimating covariance using EMPIRICAL
Done.
Number of samples used : 5070
[done]

From here, we can repeat the same steps as in the sensory section:

  • analyze eigenvalues of \(RN^{-1}\),

  • localize sources,

  • reconstruct signals with MVPURE filters,

  • and finally visualize the results.

[16]:

# Suggest number of sources to localize
# and optimization parameter to use for both localization and reconstruction
sugg_n_sources, sugg_rank = localizer.suggest_n_sources_and_rank(
    R=data_cov_task.data,
    N=noise_cov.data,
    show_plot=True,
    subject=subject,
    s=14
)
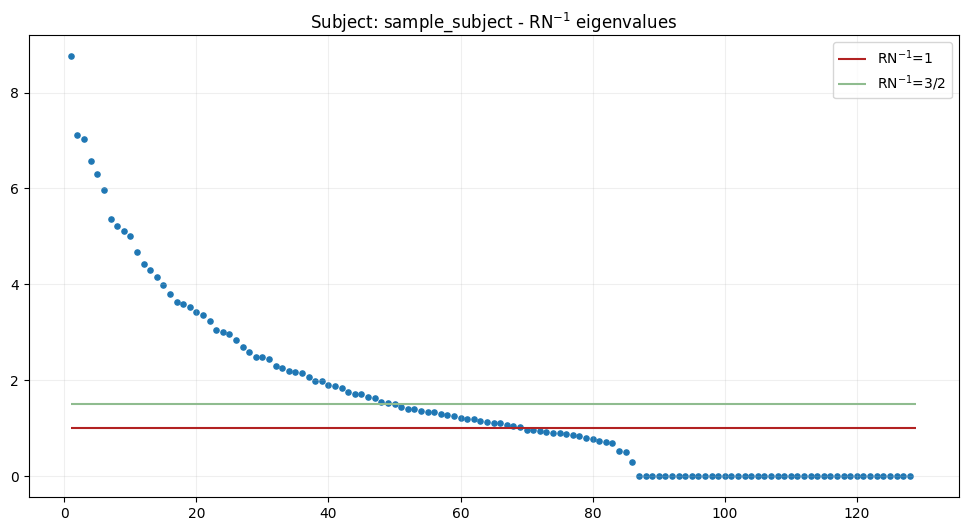
../_images/tutorials_source_localization_and_reconstruction_on_data_from_oddball_paradigm_31_0.png 
Suggested number of sources to localize: 69
Suggested rank is: 50

[17]:

# Localize
locs_task = localizer.localize(
    subject=subject,
    subjects_dir=subjects_dir,
    localizer_to_use=["mpz_mvp"],
    n_sources_to_localize=sugg_n_sources,
    R=data_cov_task.data,
    N=noise_cov.data,
    forward=fwd,
    r=sugg_rank,
)

Calculating activity index for localizer: mpz_mvp

100%|██████████| 5124/5124 [00:22<00:00, 227.29it/s]
100%|██████████| 5124/5124 [00:23<00:00, 219.92it/s]
100%|██████████| 5124/5124 [00:24<00:00, 206.87it/s]
100%|██████████| 5124/5124 [00:22<00:00, 230.55it/s]
100%|██████████| 5124/5124 [00:21<00:00, 239.85it/s]
100%|██████████| 5124/5124 [00:22<00:00, 232.09it/s]
100%|██████████| 5124/5124 [00:21<00:00, 241.26it/s]
100%|██████████| 5124/5124 [00:21<00:00, 234.91it/s]
100%|██████████| 5124/5124 [00:21<00:00, 242.70it/s]
100%|██████████| 5124/5124 [00:21<00:00, 243.91it/s]
100%|██████████| 5124/5124 [00:21<00:00, 234.48it/s]
100%|██████████| 5124/5124 [00:21<00:00, 241.44it/s]
100%|██████████| 5124/5124 [00:21<00:00, 239.30it/s]
100%|██████████| 5124/5124 [00:20<00:00, 248.39it/s]
100%|██████████| 5124/5124 [00:20<00:00, 246.96it/s]
100%|██████████| 5124/5124 [00:21<00:00, 243.96it/s]
100%|██████████| 5124/5124 [00:20<00:00, 250.55it/s]
100%|██████████| 5124/5124 [00:20<00:00, 252.83it/s]
100%|██████████| 5124/5124 [00:20<00:00, 250.98it/s]
100%|██████████| 5124/5124 [00:20<00:00, 250.03it/s]
100%|██████████| 5124/5124 [00:20<00:00, 249.71it/s]
100%|██████████| 5124/5124 [00:20<00:00, 252.17it/s]
100%|██████████| 5124/5124 [00:20<00:00, 245.33it/s]
100%|██████████| 5124/5124 [00:20<00:00, 252.36it/s]
100%|██████████| 5124/5124 [00:20<00:00, 247.02it/s]
100%|██████████| 5124/5124 [00:20<00:00, 251.69it/s]
100%|██████████| 5124/5124 [00:23<00:00, 215.61it/s]
100%|██████████| 5124/5124 [00:21<00:00, 234.60it/s]
100%|██████████| 5124/5124 [00:21<00:00, 243.44it/s]
100%|██████████| 5124/5124 [00:20<00:00, 245.63it/s]
100%|██████████| 5124/5124 [00:21<00:00, 240.35it/s]
100%|██████████| 5124/5124 [00:20<00:00, 247.86it/s]
100%|██████████| 5124/5124 [00:20<00:00, 246.37it/s]
100%|██████████| 5124/5124 [00:21<00:00, 243.88it/s]
100%|██████████| 5124/5124 [00:21<00:00, 243.70it/s]
100%|██████████| 5124/5124 [00:21<00:00, 243.27it/s]
100%|██████████| 5124/5124 [00:21<00:00, 238.34it/s]
100%|██████████| 5124/5124 [00:21<00:00, 239.47it/s]
100%|██████████| 5124/5124 [00:21<00:00, 238.29it/s]
100%|██████████| 5124/5124 [00:21<00:00, 242.33it/s]
100%|██████████| 5124/5124 [00:21<00:00, 235.48it/s]
100%|██████████| 5124/5124 [00:22<00:00, 228.16it/s]
100%|██████████| 5124/5124 [00:22<00:00, 225.14it/s]
100%|██████████| 5124/5124 [00:21<00:00, 233.82it/s]
100%|██████████| 5124/5124 [00:24<00:00, 206.37it/s]
100%|██████████| 5124/5124 [00:22<00:00, 227.36it/s]
100%|██████████| 5124/5124 [00:22<00:00, 224.77it/s]
100%|██████████| 5124/5124 [00:27<00:00, 185.77it/s]
100%|██████████| 5124/5124 [00:22<00:00, 226.67it/s]
100%|██████████| 5124/5124 [00:22<00:00, 231.82it/s]
100%|██████████| 5124/5124 [00:30<00:00, 165.56it/s]
100%|██████████| 5124/5124 [00:33<00:00, 154.77it/s]
100%|██████████| 5124/5124 [00:31<00:00, 163.60it/s]
100%|██████████| 5124/5124 [00:31<00:00, 165.03it/s]
100%|██████████| 5124/5124 [00:31<00:00, 162.19it/s]
100%|██████████| 5124/5124 [00:32<00:00, 159.90it/s]
100%|██████████| 5124/5124 [00:33<00:00, 154.72it/s]
100%|██████████| 5124/5124 [00:33<00:00, 151.46it/s]
100%|██████████| 5124/5124 [00:34<00:00, 148.82it/s]
100%|██████████| 5124/5124 [00:34<00:00, 148.85it/s]
100%|██████████| 5124/5124 [00:35<00:00, 142.92it/s]
100%|██████████| 5124/5124 [00:37<00:00, 137.03it/s]
100%|██████████| 5124/5124 [00:39<00:00, 128.70it/s]
100%|██████████| 5124/5124 [00:40<00:00, 127.15it/s]
100%|██████████| 5124/5124 [00:41<00:00, 123.43it/s]
100%|██████████| 5124/5124 [00:42<00:00, 120.62it/s]
100%|██████████| 5124/5124 [00:42<00:00, 120.70it/s]
100%|██████████| 5124/5124 [00:42<00:00, 119.88it/s]
100%|██████████| 5124/5124 [00:43<00:00, 117.34it/s]

Leadfield indices corresponding to localized sources: [1689, 1291, 1489, 2159, 4405, 5051, 2039, 800, 2020, 3224, 1792, 4998, 821, 1865, 3762, 4165, 2372, 2471, 4817, 495, 1755, 2548, 3334, 1572, 2322, 2008, 4379, 3733, 4426, 2527, 2230, 2362, 4774, 356, 2545, 902, 108, 3720, 211, 481, 64, 2740, 2303, 4641, 148, 170, 1460, 3454, 68, 4850, 1732, 641, 2310, 4678, 764, 669, 1376, 3730, 2856, 4542, 4680, 2932, 3896, 600, 3172, 2564, 2631, 4982, 1342]



[18]:

# Transform leadfield indices to vertices
lh_vert_task, lh_idx_task, rh_vert_task, rh_idx_task = utils.transform_leadfield_indices_to_vertices(
    lf_idx=locs_task["sources"],
    src=src,
    hemi="both",
    include_mapping=True
)

locs_task.add_vertices_info(
    lh_vertices=lh_vert_task,
    lh_indices=lh_idx_task,
    rh_vertices=rh_vert_task,
    rh_indices=rh_idx_task
)

[19]:

new_fwd_task = utils.subset_forward(
    old_fwd=fwd,
    localized=locs_task,
    hemi="both"
)

[20]:

mcmv_params = {
    'filter_rank': sugg_rank,
    "filter_type": "MVP_R"
}

filter_task = beamformer.make_filter(
    signal_task.info,
    new_fwd_task,
    data_cov_task,
    reg=0.05,
    noise_cov=noise_cov,
    pick_ori=None,  # because scalar forward
    weight_norm=None,
    rank=None,
    mvpure_params=mcmv_params
)

Computing rank from covariance with rank=None
    Using tolerance 5.2e-13 (2.2e-16 eps * 128 dim * 18  max singular value)
    Estimated rank (eeg): 86
    EEG: rank 86 computed from 128 data channels with 1 projector
Computing rank from covariance with rank=None
    Using tolerance 3.6e-13 (2.2e-16 eps * 128 dim * 13  max singular value)
    Estimated rank (eeg): 86
    EEG: rank 86 computed from 128 data channels with 1 projector
Making MVP_R beamformer with rank {'eeg': 86} (note: MNE-Python rank)
Computing inverse operator with 128 channels.
    128 out of 128 channels remain after picking
Selected 128 channels
Whitening the forward solution.
    Created an SSP operator (subspace dimension = 1)
Computing rank from covariance with rank={'eeg': 86}
    Setting small EEG eigenvalues to zero (without PCA)
Creating the source covariance matrix
Adjusting source covariance matrix.
Computing beamformer filters for 69 sources
MVP_R computation - in progress...
Filter rank: 50
Filter computation complete

[21]:

stc_task = beamformer.apply_filter(signal_task, filter_task)

# Add source estimate to mvpure_py.Localized object
locs_task.add_stc(stc_task)

# Plot
viz.plot_sources_with_activity(
    subject=subject,
    stc=stc_task,
)

Using control points [2.84206626e-09 3.11743662e-09 5.08812233e-09]

[21]:

<mne.viz._brain._brain.Brain at 0x16c554cd0>